One subject, three lenses: A multifaceted look at Algebra

“It is better to solve one problem five different ways than to solve five problems one way.” — George Pólya
Math lovers know a secret: there’s never just one way to solve a problem. The same idea shows up again and again, wearing different masks – as an unknown to discover, a pattern to understand, or a formula that predicts the future.
That’s the insight behind our three different Algebra courses: we want to illuminate the power of algebra from every angle.
The detective’s path: Solving Equations
In Solving Equations, you’re playing a game with one goal: find the unknown. Instead of throwing you into a sea of variables and formulas, we start with a simple physical metaphor: balance scales.
When three identical triangles balance against a 6-pound weight, the puzzle solves itself – each triangle must weigh two pounds. Suddenly, solving for \(x\) isn’t abstract – it’s a concrete puzzle with clear evidence.
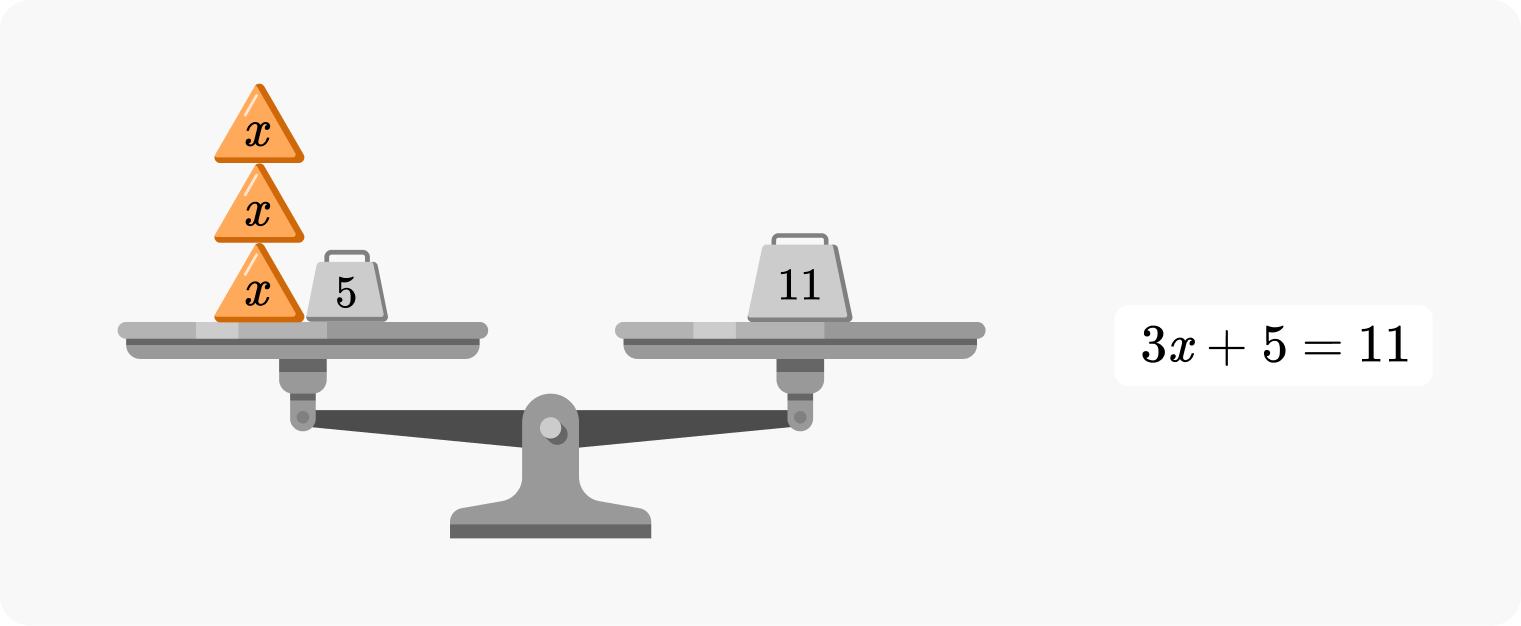
The beauty of scales is how naturally they extend to more complex versions of this same game. Tilt the scale, and you’re still finding unknowns – but now you’re discovering inequalities instead of exact values. Add another scale to the mix, and you’re hunting for multiple unknowns at once, solving systems of equations.
The puzzles evolve, but the core challenge stays laser-focused: use what you know to find what you don’t.
The pattern hunter’s journey: Visual Algebra
Visual Algebra looks at algebra from a different angle – instead of finding unknowns, we discover patterns. Here, the game is simple: find the rule.
Those variables that once stood for unknowns? Now they're stepping stones in a sequence, used to express functions – mathematical rules that generate patterns.
Take the expression \(3x + 5\): rather than solving an equation like \(3x+5=11\) you’ll use it to set up a pattern-making machine. Start with five blocks, add three at a time, and watch linear growth unfold.
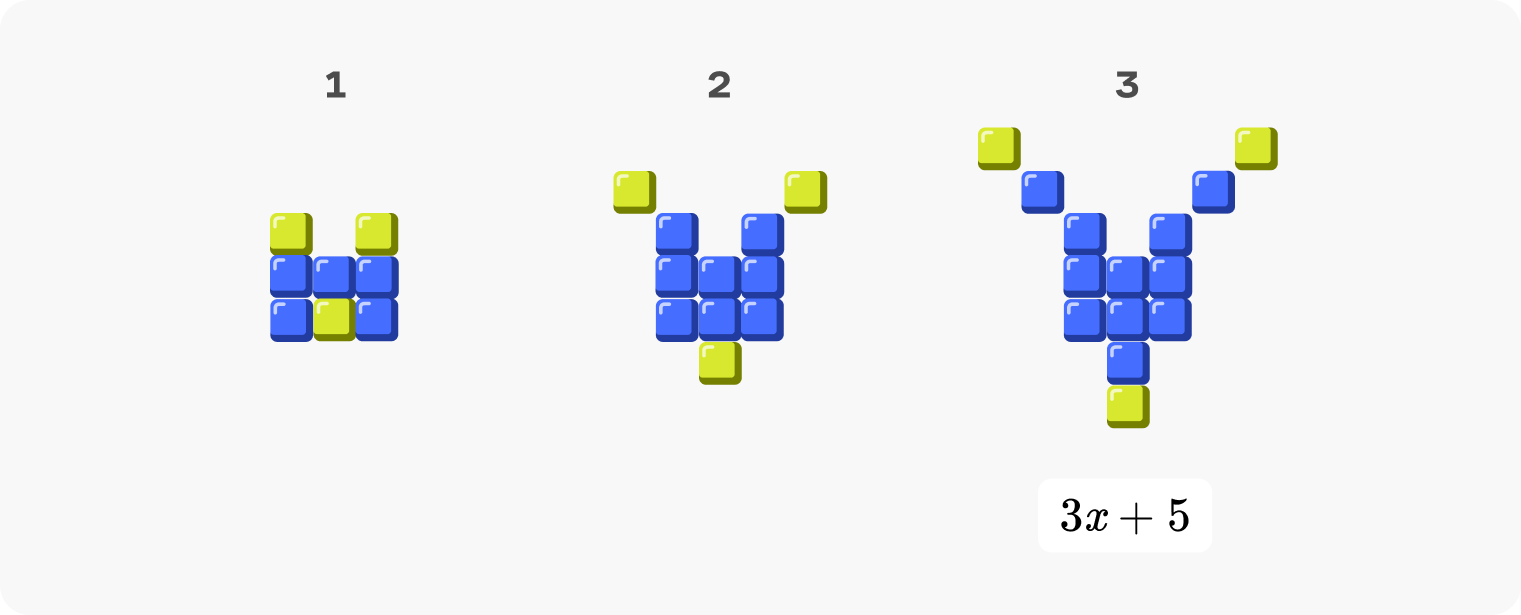
But linear patterns are just the beginning – soon you’re uncovering quadratic functions that accelerate, exponential ones that explode with growth, and even recursive patterns that feed on themselves. Each new function type reveals another way patterns can behave, but the core challenge remains the same: spot the pattern, deduce the function.
Same symbols, whole new perspective.
The pragmatist’s route: Real-World Algebra
Real-World Algebra merges these perspectives into a practical playground. Just like the other two courses, Real-World Algebra has one game: build the model.
Those variables and functions you’ve mastered? They become tools for wrestling with business data and financial forecasts. That same \(3x + 5\) might represent how you price your product or how you expect your business to grow.
You’ll craft formulas in spreadsheets, predict future values, and make smart business decisions – but now your unknowns live in tables and your patterns emerge from real data. It’s algebra in its natural habitat, where finding unknowns and spotting patterns combine to solve concrete problems.

Diving deeper into Visual Algebra
Of these three perspectives, Visual Algebra perhaps best demonstrates how gentle onramps can lead to dizzyingly complex challenges.
We start off with linear growth, patterns that start with a constant term and grow the same amount each step:
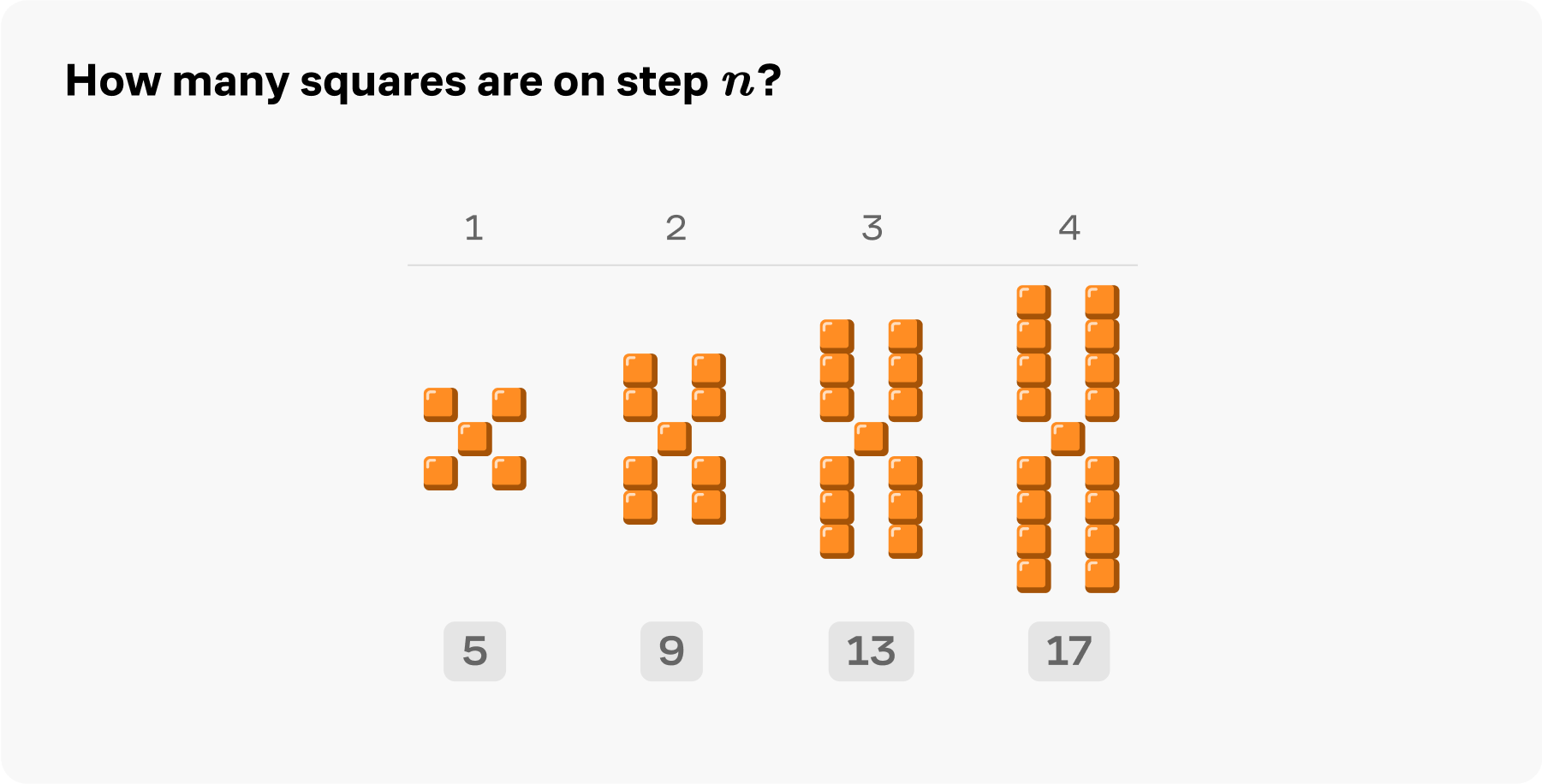
We then have you compare different rates of growth to build your familiarity with linear functions:
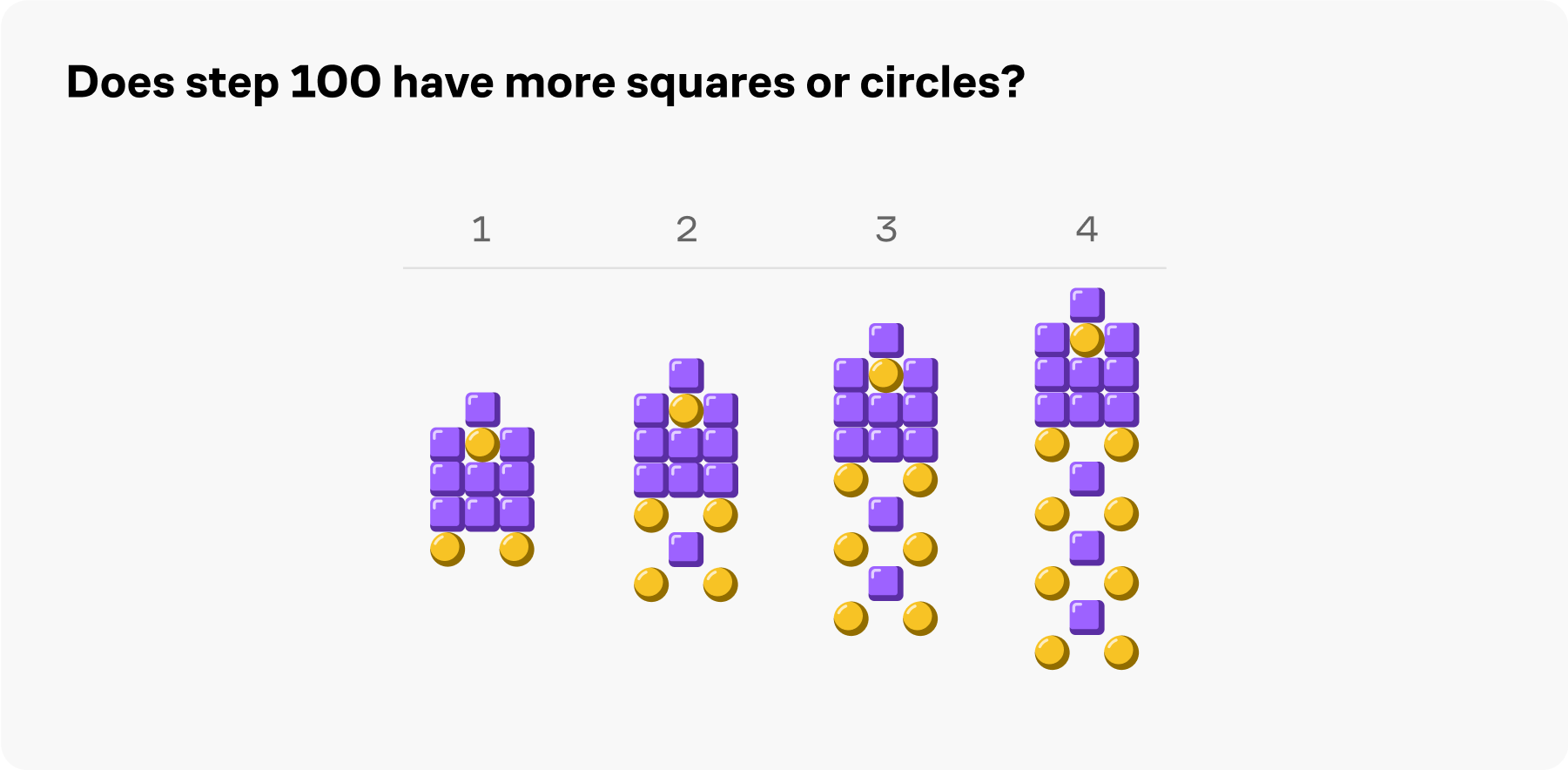
This approach makes the introduction of quadratics feel completely intuitive. They show up as really satisfying patterns that grow surprisingly quickly:
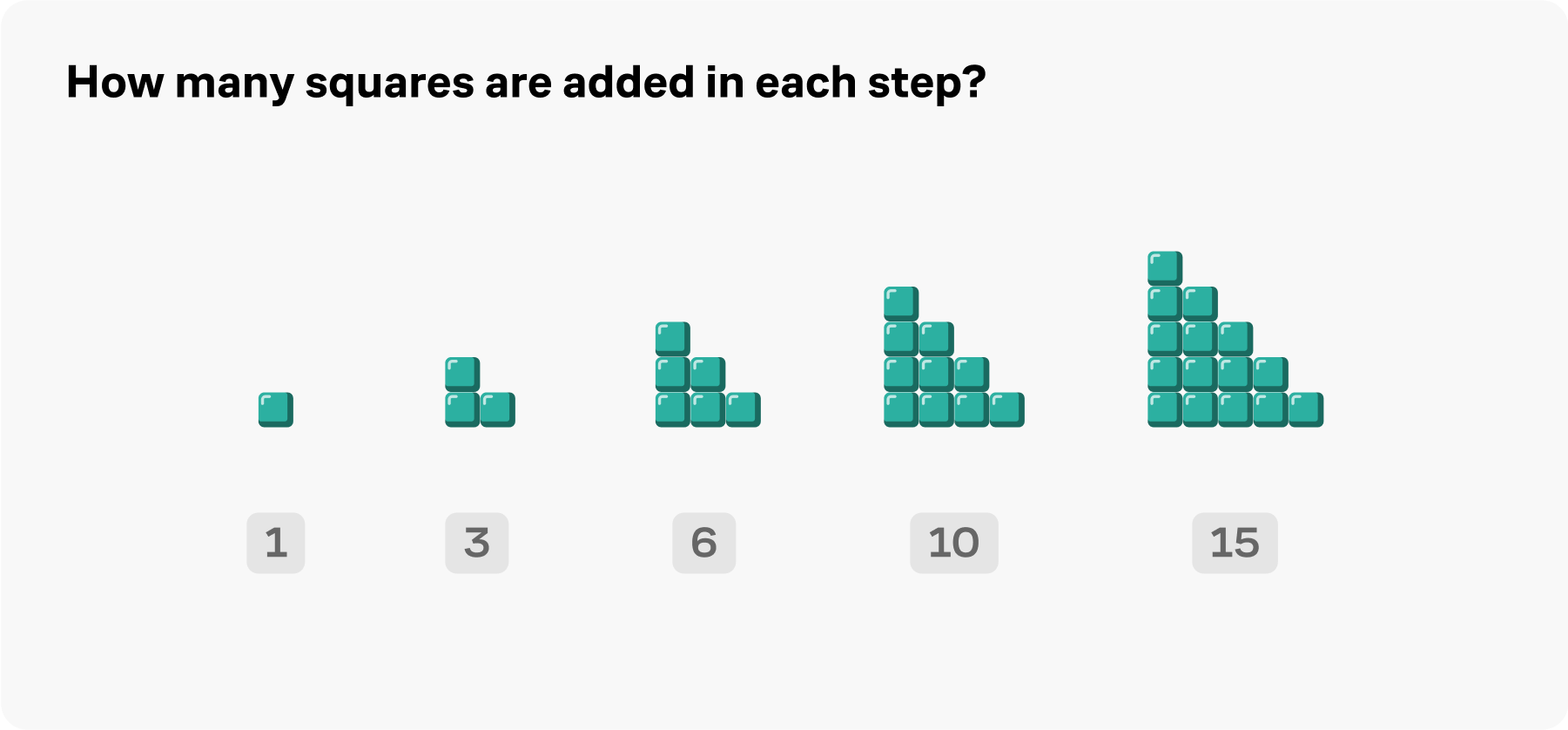
Once you’ve nailed the fundamentals, we then take you through a zoo of mathematical functions: periodic functions, exponentials, and beyond. The problems become quite diabolical, even for seasoned problem solvers.

Visual Algebra isn’t just a highlight reel of cool math concepts (although it happens to do that well, too) — it’s carefully crafted to help you see functions in a new light.
By interacting with visual patterns and deducing the rules that generate them, you’ll gain a deep, almost tactile understanding of how functions behave and what they really represent.
Pick your own pathway
Exploring algebra from these different angles is like looking at a gemstone. Each perspective reveals another facet, another flash of insight. As you turn the gem in your hand, you start to see how all those facets fit together into a single, shimmering whole.
That’s the experience our algebra courses aim to create – a multidimensional understanding of algebra that feels as natural as it is eye-opening. If you want to try it for yourself, you can get started here.
To keep up with our latest thoughts on the intersection of AI and STEM learning, follow us on LinkedIn and on X at @brilliantorg and @suekhim.

